セラミックス材料の内在欠陥

欠陥の大きさの影響

セラミック材料に亀裂(crack)、気孔(pore)、介在物(inclusion)などの欠陥(flaw)が存在すると応力集中が起こります。非延性材料中にある楕円形亀裂 (elliptical crack)の先端における応力集中は次式で示されます。$$\frac{σ_m}{σ_a}=2(\frac{c}{ρ})^{1/2}　　　・・・(1)$$ここで、σ_mは亀裂先端の最大応力、σ_aは印加した応力、2cは亀裂の長さ、ρは亀裂先端の半径になります。

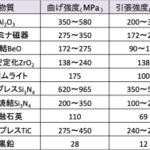
反応焼結Si₃N₄を例にしてみますが、欠陥の大きさcが170μmのときに150MPaの応力で破壊が起こったとします。亀裂先端の半径を原子間距離(2Å)に等しいと仮定し、式(1)に代入すると応力集中係数は1840となり、セラミックスでは小さな欠陥でも著しい応力集中を引き起こすことが明らかとなります。

また、破壊強度と材料の性質、及び傷の大きさを関係付ける式として式(2)も提唱されています。$$σ_f=A(\frac{Eγ}{c})^{1/2}　　　・・・(2)$$ここで、σ_fは破壊強度、Eは弾性率、γは破壊エネルギー、cは欠陥の大きさ、Aは試料や欠陥の形状で決まる定数になります。

また、式(2)をより一般化した関係も提案されています。$$σ_f=\frac{Z}{Y}(\frac{2Eγ}{c})^{1/2}　　　・・・(2)$$ここで、Yは欠陥の深さと試験片の形状で決まる無次元項、Zは欠陥の配置で決まる別の無次元項、cは表面の欠陥の深さ(あるいは内部欠陥の寸法の半分)で、Eやγは式(2)のときと同じになります。引張り応力下で断面積の1/10以下の寸法の内部欠陥については Y = 1.77になります。曲げ応力下で断面の厚さの1/10よりずっと小さな寸法の表面欠陥ではYは2.0に近づきます。Zの値は欠陥の形状で変化し一般に1.0〜2.0の間の値をとります。

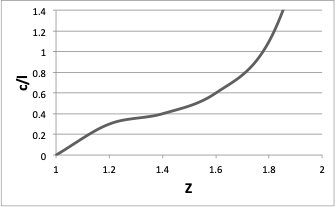
セラミックスの表面にある平面的な楕円形亀裂による影響は解析が容易です。この種の欠陥は機械加工、衝撃、熱衝撃、釉薬の亀裂その他の原因によって発生します。Zの値は欠陥の深さcと長さlの比によって、図1のように変化します。

気孔や介在物等による三次元的な欠陥による影響は二次元の場合ほど厳密に扱われていませんが、強度は以下の諸因子によって影響されます。